Getting Started Programming with Qt Widgets¶
A tutorial for Qt Widgets based on a notepad application.
In this topic, we teach basic Qt knowledge by implementing a simple Notepad application using C++ and the Qt Widgets module. The application is a small text editor which allows you to create a text file, save it, print it, or reopen and edit it again. You can also set the font to be used.
You can find the final Notepad source files in the qtdoc repository in the tutorials/notepad directory. You can either fetch the Qt 5 sources from Qt Project or install them as part of Qt 5. The application is also available in the example list of Qt Creator’s Welcome mode.
Creating the Notepad Project¶
Setting up a new project in Qt Creator is aided by a wizard that guides you step-by-step through the project creation process. The wizard prompts you to enter the settings needed for that particular type of project and creates the project for you.
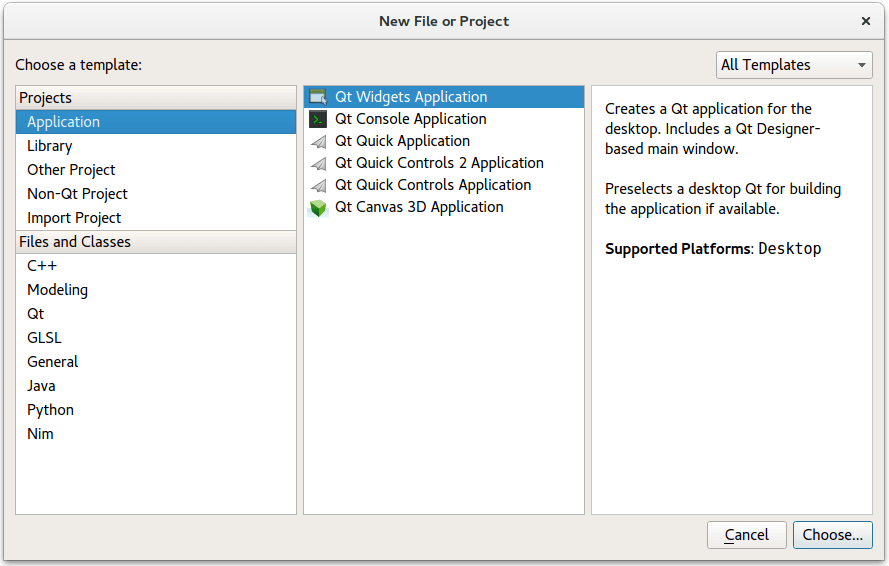
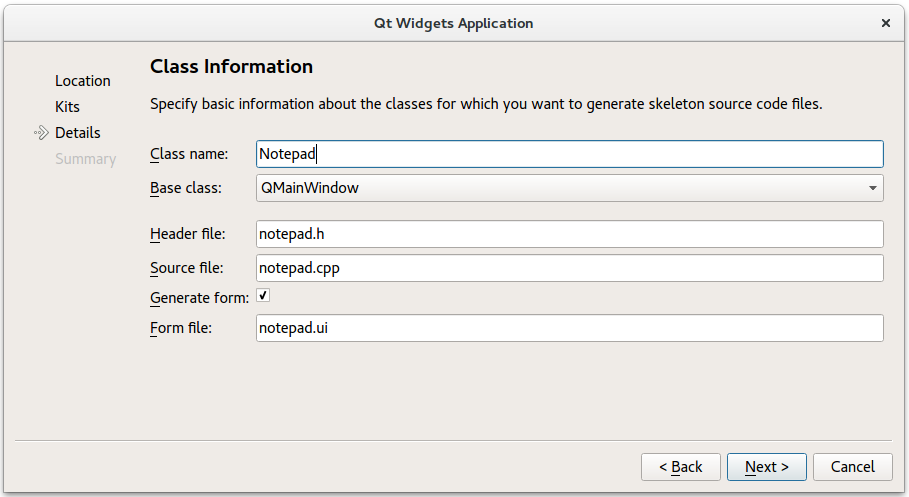
To create the Notepad project, select File > New File or Project > Applications > Qt Widgets Application > Choose , and follow the instructions of the wizard. In the Class Information dialog, type Notepad as the class name and select QMainWindow as the base class.
The Qt Widgets Application wizard creates a project that contains a main source file and a set of files that specify a user interface (Notepad widget):
notepad.pro - the project file.
main.cpp - the main source file for the application.
notepad.cpp - the source file of the notepad class of the Notepad widget.
notepad.h - the header file of the notepad class for the Notepad widget.
notepad.ui - the UI form for the Notepad widget.
The .cpp, .h, and .ui files come with the necessary boiler plate code for you to be able to build and run the project. The .pro file is complete. We will take a closer look at the file contents in the following sections.
Learn More
About
Here
Using Qt Creator
Qt Creator
Creating other kind of applications with Qt Creator
Qt Creator Tutorials
Main Source File¶
The wizard generates the following code in the main.cpp file:
We will go through the code line by line. The following lines include the header files for the Notepad widget and
QApplication. All Qt classes have a header file named after them.The following line defines the main function that is the entry point for all C and C++ based applications:
The following line creates a
QApplicationobject. This object manages application-wide resources and is necessary to run any Qt program that uses Qt Widgets. It constructs an application object withargccommand line arguments run inargv. (For GUI applications that do not use Qt Widgets, you can useQGuiApplicationinstead.)The following line creates the Notepad object. This is the object for which the wizard created the class and the UI file. The user interface contains visual elements that are called
widgetsin Qt. Examples of widgets are text edits, scroll bars, labels, and radio buttons. A widget can also be a container for other widgets; a dialog or a main application window, for example.The following line shows the Notepad widget on the screen in its own window. Widgets can also function as containers. An example of this is
QMainWindowwhich often contains several types of widgets. Widgets are not visible by default; the functionshow()makes the widget visible.The following line makes the
QApplicationenter its event loop. When a Qt application is running, events are generated and sent to the widgets of the application. Examples of events are mouse presses and key strokes.Learn More
About
Here
Widgets and Window Geometry
Events and event handling
Designing a UI¶
The wizard generates a user interface definition in XML format: notepad.ui. When you open the notepad.ui file in Qt Creator, it automatically opens in the integrated Qt Designer.
When you build the application, Qt Creator launches the Qt User Interface Compiler (uic) that reads the .ui file and creates a corresponding C++ header file, ui_notepad.h.
Using Qt Designer¶
The wizard creates an application that uses a
QMainWindow. It has its own layout to which you can add a menu bar, dock widgets, toolbars, and a status bar. The center area can be occupied by any kind of widget. The wizard places the Notepad widget there.To add widgets in Qt Designer:
In the Qt Creator Editor mode, double-click the notepad.ui file in the Projects view to launch the file in the integrated Qt Designer.
Drag and drop widgets Text Edit (
QTextEdit) to the form.Press Ctrl+A (or Cmd+A) to select the widgets and click Lay out Vertically (or press Ctrl+L) to apply a vertical layout (
QVBoxLayout).Press Ctrl+S (or Cmd+S) to save your changes.
The UI now looks as follows in Qt Designer:
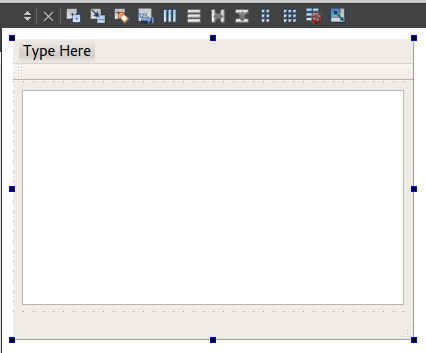
You can view the generated XML file in the code editor:
...The following line contains the XML declaration, which specifies the XML version and character encoding used in the document:
<?xml version="1.0" encoding="UTF-8"?>The rest of the file specifies an
uielement that defines a Notepad widget:<ui version="4.0">The UI file is used together with the header and source file of the Notepad class. We will look at the rest of the UI file in the later sections.
Notepad Header File¶
The wizard generated a header file for the Notepad class that has the necessary #includes, a constructor, a destructor, and the Ui object. The file looks as follows:
#include <QMainWindow> QT_BEGIN_NAMESPACE namespace Ui { class Notepad; } QT_END_NAMESPACE class Notepad : public QMainWindow { Q_OBJECT public: explicit Notepad(QWidget *parent = nullptr); ~Notepad(); private slots: void newDocument(); void open(); void save(); void saveAs(); void print(); void exit(); void copy(); void cut(); void paste(); void undo(); void redo(); void selectFont(); void setFontBold(bool bold); void setFontUnderline(bool underline); void setFontItalic(bool italic); void about(); private: Ui::Notepad *ui; QString currentFile; };The following line includes
QMainWindowthat provides a main application window:#include <QMainWindow>The following lines declare the Notepad class in the Ui namespace, which is the standard namespace for the UI classes generated from .ui files by the
uictool:QT_BEGIN_NAMESPACE namespace Ui { class Notepad; } QT_END_NAMESPACEThe class declaration contains the
Q_OBJECTmacro. It must come first in the class definition, and declares our class as aQObject. Naturally, it must also inherit fromQObject. AQObjectadds several abilities to a normal C++ class. Notably, the class name and slot names can be queried at runtime. It is also possible to query a slot’s parameter types and invoke it.class Notepad : public QMainWindow { Q_OBJECTThe following lines declare a constructor that has a default argument called
parent. The value 0 indicates that the widget has no parent (it is a top-level widget).public: explicit Notepad(QWidget *parent = nullptr);The following line declares a virtual destructor to free the resources that were acquired by the object during its life-cycle. According to the C++ naming convention, destructors have the same name as the class they are associated with, prefixed with a tilde (~). In
QObject, destructors are virtual to ensure that the destructors of derived classes are invoked properly when an object is deleted through a pointer-to-base-class.~Notepad();The following lines declare a member variable which is a pointer to the Notepad UI class. A member variable is associated with a specific class, and accessible for all its methods.
private: Ui::Notepad *ui; QString currentFile;
Notepad Source File¶
The source file that the wizard generated for the Notepad class looks as follows:
The following lines include the Notepad class header file that was generated by the wizard and the UI header file that was generated by the
uictool:The following line defines the
Notepadconstructor:The following line calls the
QMainWindowconstructor, which is the base class for the Notepad class:The following line creates the UI class instance and assigns it to the
uimember:The following line sets up the UI:
In the destructor, we delete the
ui:In order to have the text edit field occupy the whole screen, we add
setCentralWidgetto the main window.
Project File¶
The wizard generates the following project file,
notepad.pro, for us:<Code snippet "/data/snapshot-qt5full-5.15/qt5/qtbase/tutorials/notepad/notepad.pro" not found>The project file specifies the application name and the
qmaketemplate to use for generating the project, as well as the source, header, and UI files included in the project.You could also use
qmake‘s-projectoption to generate the .pro file. Although, in that case, you have to remember to add the lineQT += widgetsto the generated file in order to link against the Qt Widgets Module.Learn More
About
Here
Using Qt Designer
Qt Designer Manual
Layouts
The widgets that come with Qt
Main windows and main window classes
Application Main Window , Main Window Examples
QObjects and the Qt Object model (This is essential to understand Qt)
qmake and the Qt build system
qmake Manual
Adding User Interaction¶
To add functionality to the editor, we start by adding menu items and buttons on a toolbar.
Click on “Type Here”, and add the options New, Open, Save, Save as, Print and Exit. This creates 5 lines in the Action Editor below. To connect the actions to slots, right-click an action and select Go to slot > triggered(), and complete the code for that given slot.
If we also want to add the actions to a toolbar, we can assign an icon to each
QAction, and then drag theQActionto the toolbar. You assign an icon by entering an icon name in the Icon property of the action concerned. When theQActionhas been dragged to the toolbar, clicking the icon will launch the associated slot.Complete the method
newDocument():
current_fileis a global variable containing the file presently being edited. It is defined in the private part of notepad.h:
clear()clears the text buffer.
Opening a file¶
In
notepad.ui, right click onactionOpenand selectGo to slotComplete method
open().
QFileDialog::getOpenFileNameopens a dialog enabling you to select a file.QFileobjectmyfilehas the selectedfile_nameas parameter. We store the selected file also into the global variablecurrent_filefor later purposes. We open the file withfile.openas a readonly text file. If it cannot be opened, a warning is issued, and the program stops.We define a
QTextStreaminstreamfor parametermyfile. The contents of filemyfileis copied intoQStringtext.setText(text)fille the buffer of our editor withtext.
section2Saving a fileWe create the method for saving a file in the same way as for Opening a file , by right clicking on
actionSave, and selectingGo to Slot.
QFileobjectmyfileis linked to global variablecurrent_file, the variable that contains the file we were working with. If we cannot openmyfile, an error message is issued and the method stops. We create aQTextStreamoutstream. The contents of the editor buffer is converted to plain text, and then written tooutstream.
Saving a file with
Save as
This is the same procedure as for
Saving a file, the only difference being that here you need to enter a new file name for the file to be created.
Print a File¶
If you want to use print functionalities, you need to add
printsupportto the project file:QT += printsupportWe declare a
QPrinterobject calledprinter. We launch a printer dialog box and store the selected printer in objectprinter. If we clicked onCanceland did not select a printer, the methods returns. The actual printer command is given withui->textEdit->printwith ourQPrinterobject as parameter.
Select a Font¶
We declare a boolean indicating if we did select a font with
QFontDialog. If so, we set the font withui->textEdit->setFont(myfont).
Copy, Cut, Paste, Undo, and Redo¶
If you select some text, and want to copy it to the clipboard, you call the appropriate method of ui->textEdit. The same counts for cut, paste, undo, and redo.
This table shows the method name to use.
Task
Method called
Copy
ui->textEdit->copy()
Cut
ui->textEdit->cut()
Paste
ui->textEdit->paste()
Undo
ui->textEdit->undo()
Redo
ui->textEdit->redo()
Learn More
About
Here
MDI applications
QMdiArea, MDI ExampleFiles and I/O devices
QFile,QIODevicetr() and internationalization
Qt Linguist Manual, Writing Source Code for Translation, Internationalization with Qt
Building and Running Notepad¶
Now that you have all the necessary files, select Build > Build Project Notepad to build and run the application. Qt Creator uses
qmakeandmaketo create an executable in the directory specified in the build settings of the project and runs it.
Building and Running from the Command Line¶
To build the application from the command line, switch to the directory in which you have the
.cppfile of the application and add the project file (suffixed .pro) described earlier. The following shell commands then build the application:qmake make (or nmake on Windows)The commands create an executable in the project directory. The
qmaketool reads the project file and produces aMakefilewith instructions on how to build the application. Themaketool (or thenmaketool) then reads theMakefileand produces the executable binary.
© 2022 The Qt Company Ltd. Documentation contributions included herein are the copyrights of their respective owners. The documentation provided herein is licensed under the terms of the GNU Free Documentation License version 1.3 as published by the Free Software Foundation. Qt and respective logos are trademarks of The Qt Company Ltd. in Finland and/or other countries worldwide. All other trademarks are property of their respective owners.
