Qt Quick 3D - カスタムモーフィングアニメーション

モーフターゲットを持つC++カスタムジオメトリの書き方を説明します。

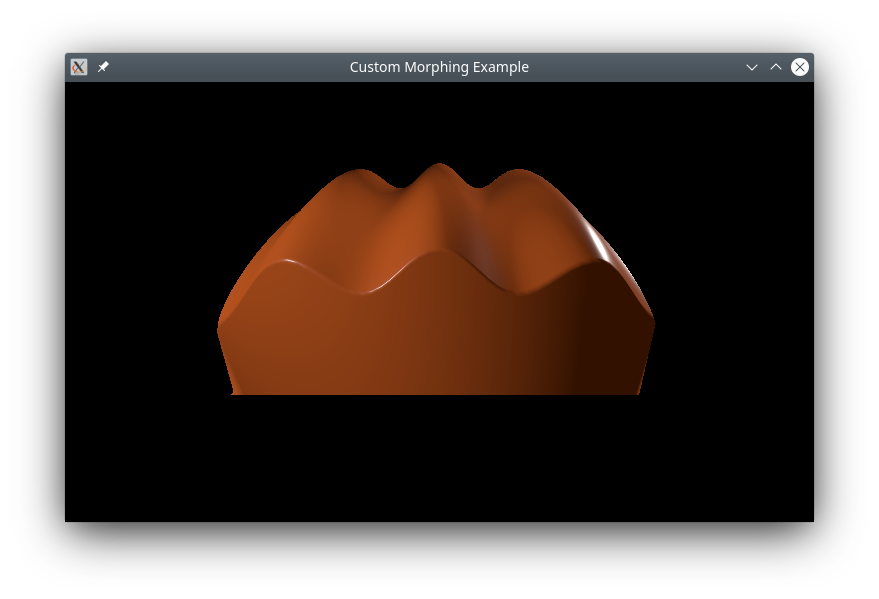
この例では、ベースシェイプとモーフターゲットを含む複雑なカスタムジオメトリをC++で定義する方法を示します。

カスタムジオメトリ

この例の主な部分は、モーフターゲットを持つカスタムジオメトリを作成することです。これはQQuick3DGeometry をサブクラス化することで行います：

class MorphGeometry : public QQuick3DGeometry
{
    Q_OBJECT
    QML_NAMED_ELEMENT(MorphGeometry)
    Q_PROPERTY(int gridSize READ gridSize WRITE setGridSize NOTIFY gridSizeChanged)

public:
    MorphGeometry(QQuick3DObject *parent = nullptr);

    int gridSize() { return m_gridSize; }
    void setGridSize(int gridSize);

signals:
    void gridSizeChanged();

private:
    void calculateGeometry();
    void updateData();

    QList<QVector3D> m_positions;
    QList<QVector3D> m_normals;
    QList<QVector4D> m_colors;

    QList<QVector3D> m_targetPositions;
    QList<QVector3D> m_targetNormals;
    QList<QVector4D> m_targetColors;

    QList<quint32> m_indexes;

    QByteArray m_vertexBuffer;
    QByteArray m_indexBuffer;
    QByteArray m_targetBuffer;

    int m_gridSize = 50;
    QVector3D boundsMin;
    QVector3D boundsMax;
};

コンストラクタはメッシュデータのレイアウトを定義します：

MorphGeometry::MorphGeometry(QQuick3DObject *parent)
    : QQuick3DGeometry(parent)
{
    updateData();
}

関数updateData はメッシュジオメトリの実際のアップロードを実行します：

void MorphGeometry::updateData()
{
    clear();
    calculateGeometry();

    addAttribute(QQuick3DGeometry::Attribute::PositionSemantic, 0,
                 QQuick3DGeometry::Attribute::ComponentType::F32Type);
    addAttribute(QQuick3DGeometry::Attribute::NormalSemantic, 3 * sizeof(float),
                 QQuick3DGeometry::Attribute::ComponentType::F32Type);
    addAttribute(QQuick3DGeometry::Attribute::ColorSemantic, 6 * sizeof(float),
                 QQuick3DGeometry::Attribute::ComponentType::F32Type);

    addTargetAttribute(0, QQuick3DGeometry::Attribute::PositionSemantic, 0);
    addTargetAttribute(0, QQuick3DGeometry::Attribute::NormalSemantic, m_targetPositions.size() * sizeof(float) * 3);
    addTargetAttribute(0, QQuick3DGeometry::Attribute::ColorSemantic,
                       m_targetPositions.size() * sizeof(float) * 3 + m_targetNormals.size() * sizeof(float) * 3);
    addAttribute(QQuick3DGeometry::Attribute::IndexSemantic, 0,
                 QQuick3DGeometry::Attribute::ComponentType::U32Type);

    const int numVertexes = m_positions.size();
    m_vertexBuffer.resize(numVertexes * sizeof(Vertex));
    Vertex *vert = reinterpret_cast<Vertex *>(m_vertexBuffer.data());

    for (int i = 0; i < numVertexes; ++i) {
        Vertex &v = vert[i];
        v.position = m_positions[i];
        v.normal = m_normals[i];
        v.color = m_colors[i];
    }
    m_targetBuffer.append(QByteArray(reinterpret_cast<char *>(m_targetPositions.data()), m_targetPositions.size() * sizeof(QVector3D)));
    m_targetBuffer.append(QByteArray(reinterpret_cast<char *>(m_targetNormals.data()), m_targetNormals.size() * sizeof(QVector3D)));
    m_targetBuffer.append(QByteArray(reinterpret_cast<char *>(m_targetColors.data()), m_targetColors.size() * sizeof(QVector4D)));

    setStride(sizeof(Vertex));
    setVertexData(m_vertexBuffer);
    setTargetData(m_targetBuffer);
    setPrimitiveType(QQuick3DGeometry::PrimitiveType::Triangles);
    setBounds(boundsMin, boundsMax);

    m_indexBuffer = QByteArray(reinterpret_cast<char *>(m_indexes.data()), m_indexes.size() * sizeof(quint32));
    setIndexData(m_indexBuffer);
}

コンストラクタからupdateData を呼び出し、プロパティが変更されたときに呼び出します。

関数calculateGeometry には、形状と法線ベクトルを計算するための面倒な数学がすべて含まれています。これはこの例に特有のもので、コードの詳細は説明しません。一般的に：滑らかなシェーディングを実装するには、各頂点の法線ベクトルを計算する必要があります。数学的には、法線ベクトルは平面を記述する関数の偏導関数から計算できます：

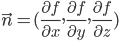
この例では、基本形状に余弦波を使用し、その導関数が正弦関数であることを知っていることで、簡単にしています。

実際には、法線ベクトルは幾何学的な推論によって決定できることが多い。モーフターゲットでは、球の中心から表面へのベクトルが、その点での球の法線になるという事実を使う。QtQuick3D の法線ベクトルは長さが単位でなければならないことに注意してください。これはQVector3D::normalized() を使うことで可能です。

QMLパート

カスタムジオメトリで作成したモーフターゲットに対応するモーフターゲットを定義し、ウェイトでアニメーションを行い、2つの形状の間を循環するようにします：

MorphTarget {
    id: morphtarget
    attributes: MorphTarget.Position | MorphTarget.Normal | MorphTarget.Color
    SequentialAnimation on weight {
        PauseAnimation { duration: 1000 }
        NumberAnimation { from: 0; to: 1; duration: 4000 }
        PauseAnimation { duration: 1000 }
        NumberAnimation { from: 1; to: 0; duration: 4000 }
        loops: Animation.Infinite
    }
}

最後に、カスタムジオメトリを使ってモデルを作成し、モーフターゲットを適用します：

Model {
    y: -1
    geometry: MorphGeometry {}
    morphTargets: [ morphtarget ]
    materials: [ material ]
}

プロジェクト例 @ code.qt.io

© 2025 The Qt Company Ltd. Documentation contributions included herein are the copyrights of their respective owners. The documentation provided herein is licensed under the terms of the GNU Free Documentation License version 1.3 as published by the Free Software Foundation. Qt and respective logos are trademarks of The Qt Company Ltd. in Finland and/or other countries worldwide. All other trademarks are property of their respective owners.